公式の理解と反復学習が肝心！高校数学の勉強法

高校数学は中学時代の数学から一気に内容が難しくなるため、ただ公式を丸暗記しただけでは対処が難しく、頭を抱えている大学受験生もいらっしゃるのではないでしょうか。

高校数学をマスターできるかは、公式を本質的に理解した上で、反復学習の習慣を身につけられるか否かに懸かっているのです。

そこで今回は、高校数学において重要な公式を覚えるための、プロ家庭教師よる3つのコツについてご紹介します。

高校数学の勉強法にお悩みの大学受験生の方は、ぜひ参考にしてください。

「高校数学の勉強法＝公式の丸暗記」はNG！

高校数学では、公式を覚えなければ解けない問題が多くを占めています。

このことから多くの受験生が「公式さえ覚えておけば何とかなる」という誤った認識に陥りがちです。

しかし、どんなに公式を丸暗記したとしても、次の単元に入ればすぐ忘れるかもしれません。

ただ暗記するだけでは、うまく応用できないのです。

これでは大学受験で苦労することが目に見えています。

数学の公式をきちんと身につけるための学習をするには、以下の3点を意識してみましょう。

1.公式の意味を理解する

2.実際に公式を使って例題を解いてみる（反復する）

3.関連した公式を合わせて覚える

公式の理解が必要であることを踏まえ、高校数学の勉強法をご紹介します。

公式の本質を理解するには？

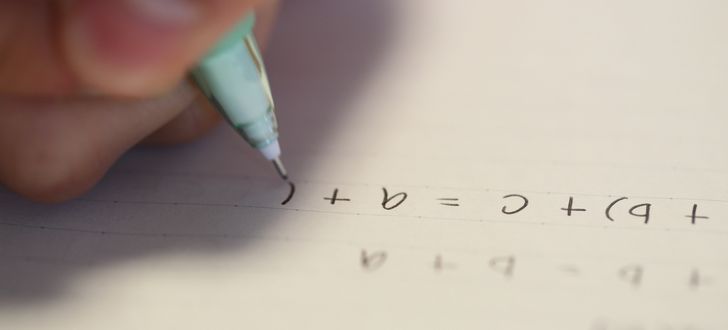
数学の公式は、意味を理解したり関連する公式を組み合わせたりすると、より覚えやすくなります。

先にご紹介した「1.公式の意味を理解する」、「3.関連した公式を合わせて覚える」の組み合わせです。


例えば、数学で頻出の「等差数列」で、公式を理解するコツを見ていきましょう。

等差数列とは、「最初の数（初項）に一定の数（公差）を足し続けた場合の数列」を指します。

以下の数列をご参照ください。

3, 7, 11, 15, 19, 23, 27……

上の数列は、初項3に、公差4を足し続けたものです。

等差数列の問題で多いケースは、「等差中項」を求めるものです。

等差中項の公式は、等差数列において「a, b, c」という数字の列がある場合、

「b＝（a＋c）÷2（あるいは2b＝a＋c）」となります。

この場合、公式をただ丸暗記するのではなく、「等差中項とは何を求めるのか」を考えなければなりません。

等差中項とは、「等差数列において連続する3つの数列の、右端の数と左端の数を足すと、真ん中の数の2倍になる」ということです。

例えば、上記の数列で「7,11,15」を取り上げるとすると、「11＝（7＋15）÷2」ということになります。

等差中項の問題が出たときに、「等差中項とは、数列の右端と左端を足すと、真ん中の2倍になるということだったな」と思い出すことができれば、

「b＝（a＋c）÷2」という公式が導き出せます。

これが、「公式の意味まで理解する」ということです。

等差中項を覚えるときは、「等比中項」も一緒に覚えると効率的なのでおすすめします。

等比中項の公式は、「bの2乗＝ac」あるいは「b＝±√ac」ですが、

これも「等比中項とは、両端の数字をかけると真ん中の数字の2乗になる」と覚えれば、すぐ公式が導き出せます。

高校数学は反復学習が成否を握る

数学の公式はただ覚えるのではなく、「気づいたら使いこなせていた」という状態まで落とし込むことが理想です。

そのためには、やはり反復学習が欠かせません。

人間の脳は、同じ行動を繰り返せば「この情報は覚えよう」と判断するようになります。

しかも反復学習は、脳の処理スピードをより速くすることにも役立つため、1問にかける時間が短くなり、受験本番でも有利になるでしょう。

数学は積み重ねの教科です。

「新しい公式を覚えたら以前習った公式を忘れてしまった」では意味がありません。

公式を覚えたら翌日に復習し、3日後にまた復習し、さらに1週間後にも復習し……と、定着しているか反復してチェックしましょう。

地味ではありますが、反復学習こそが数学の力をつける近道です。

おわりに

今回は高校数学の勉強法として、公式の理解と反復学習の重要性をご紹介しました。

高校数学では複雑な公式が多いため、丸暗記では大学入試はおろか高校の定期テストですら太刀打ちできません。

公式を理解した上で反復学習を心がけましょう。

また、独学での学習に限界があると感じるなら、プロ家庭教師によるオンライン指導を検討することも一案です。

全国どこからでも、最新の受験ノウハウを身につけたプロ家庭教師の指導が受けられる「メガスタ」が、数学を確実な得点源にできるよう指導します。